library(tidyverse)
library(tidymodels)
library(ggcorrplot)11 Fallstudie Vorhersagemodellierung Iris
11.1 Was ist ein lineares Modell?
Jetzt, da wir unsere Daten in der EDA aufbereitet und Anomalien beseitigt haben, können wir uns an einer Vorhersage versuchen. Hierzu bedienen wir uns an einem linearen Modell, das heißt, wir legen eine Gerade über die Punktewolke unserer AV und versuchen, die Abstände von den Punkten, also den echten Werten zu der Gerade, welche die vorhergesagten Werte darstellt, zu minimieren. Um ein lineares Modell zu erstellen, benutzen wir einfach den Befehl lm().
data(iris)
#Aufteilen der Daten in train und test sample, Erstellen einer ID-Spalte (Für die Klausur irrelevant:)
iris <- iris %>%
mutate(id = row_number()) %>%
select(id, everything())
set.seed(123)
train_test_split <- initial_split(iris, prop = 0.7)
iris_train <- training(train_test_split)
iris_test <- testing(train_test_split)11.2 Erstellen eines einfachen linearen Modells
11.2.1 Variablenauswahl
Wenn wir jetzt im Iris Datensatz Sepal.Length vorhersagen wollen, müssen wir zuerst überlegen, welche Variablen uns dabei als Prädiktoren dienen könnten. Ein Anhaltspunkt ist der Korrelationsplot, den wir im letzten Kapitel erstellt haben.
iris_train %>%
select(where(is.numeric)) %>%
cor() %>%
ggcorrplot(method = "circle",
type = "lower",
colors = c("violet", "grey", "blue"))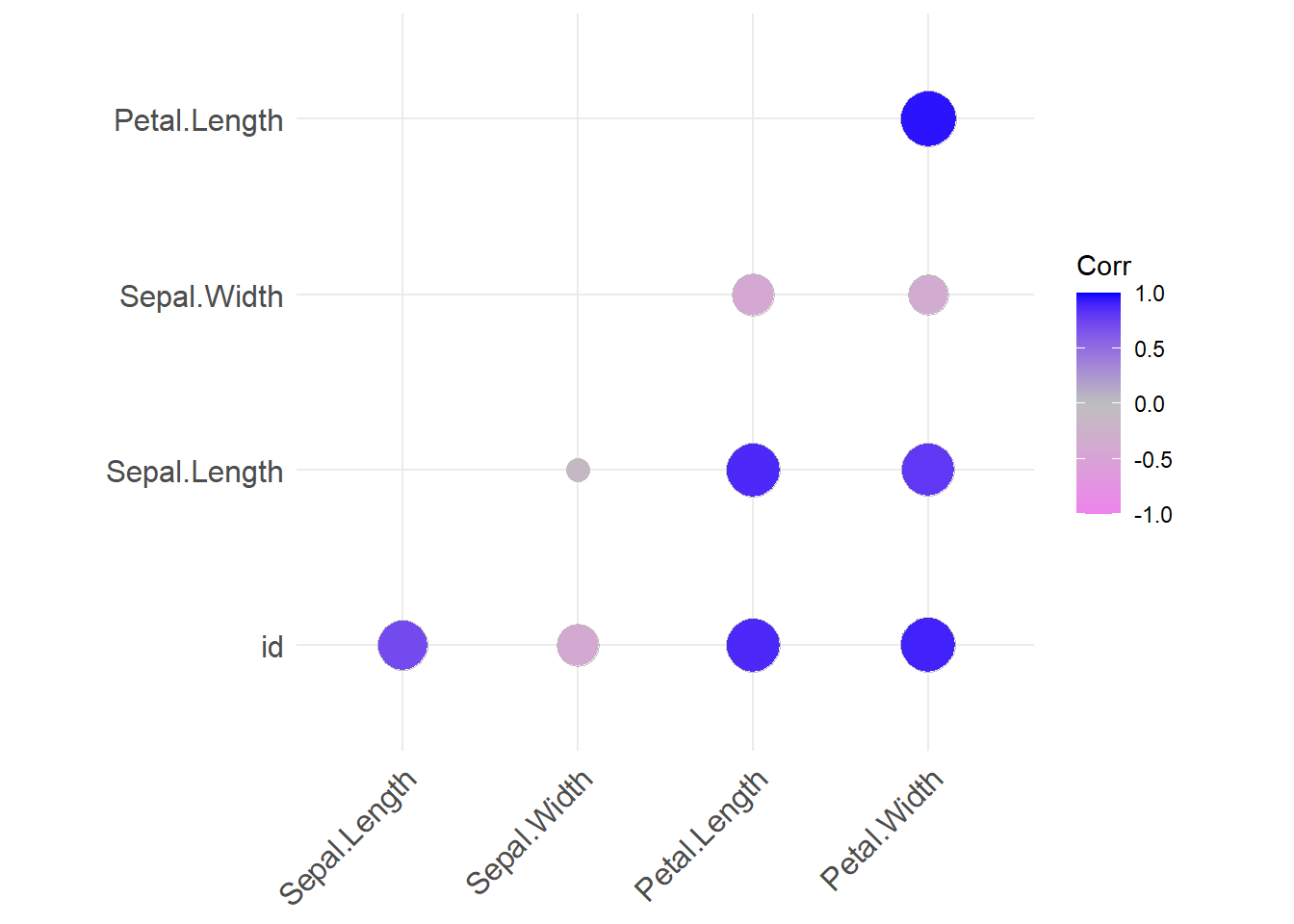
Hier können wir deutlich sehen, dass sowohl Petal.Length als auch Petal.Width, einen starken Zusammenhang mit Sepal.Length aufweisen. Anders gesagt: Je länger und breiter das Kelchblatt einer Blüte ist, desto länger ist das Blütenblatt.
11.2.2 Erstellen des Modells
Der Einfachheit halber nehmen wir erstmal nur einen Prädiktor, nämlich Sepal.Length:
lm1 <- lm(Sepal.Length ~ Petal.Length,
data = iris_train)Mit nur einem Prädiktor lässt sich das Modell auch noch leicht visualisieren:
ggplot(iris_train, aes(x = Petal.Length, y = Sepal.Length)) +
geom_point() +
geom_smooth(method = lm)`geom_smooth()` using formula = 'y ~ x'
11.2.3 Ausgeben der Metrics
Wenn wir jetzt wissen wollen, wie gut unser Modell ist, können wir uns mit summary()eine Zusammenfassung aller Kennwerte des Modells ausgeben lassen:
summary(lm1)
Call:
lm(formula = Sepal.Length ~ Petal.Length, data = iris_train)
Residuals:
Min 1Q Median 3Q Max
-1.25703 -0.31710 -0.03212 0.24553 1.04518
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.24492 0.09642 44.02 <2e-16 ***
Petal.Length 0.42491 0.02314 18.36 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4247 on 103 degrees of freedom
Multiple R-squared: 0.7661, Adjusted R-squared: 0.7638
F-statistic: 337.3 on 1 and 103 DF, p-value: < 2.2e-16Fürs Erste schauen wir uns nur den Wert für das Adjusted R-squared an. Dieser sagt uns, dass rund 76% der Varianz von Petal.Length durch Sepal.Length erklärt werden kann. Zur Vertiefung von R2 ist folgendes Video gut geeignet:
StatQuest: Linear Models
11.3 Erstellen eines Modells mit mehreren Prädiktoren
lm2 <- lm(Sepal.Length ~ Petal.Length + Petal.Width,
data = iris_train)summary(lm2)
Call:
lm(formula = Sepal.Length ~ Petal.Length + Petal.Width, data = iris_train)
Residuals:
Min 1Q Median 3Q Max
-1.16585 -0.31081 -0.06377 0.27233 1.06452
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.0925 0.1150 35.596 < 2e-16 ***
Petal.Length 0.6126 0.0839 7.302 6.41e-11 ***
Petal.Width -0.4609 0.1983 -2.324 0.0221 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4159 on 102 degrees of freedom
Multiple R-squared: 0.7778, Adjusted R-squared: 0.7735
F-statistic: 178.5 on 2 and 102 DF, p-value: < 2.2e-16Das adj R2 ist nur minimal gestiegen. Zum Glück gibt es noch andere Methoden, um unsere Vorhersagegüte zu erhöhen. Im Folgenden werden wir auf eine kleine Auswahl dieser Methoden eingehen.
11.4 Methoden zur Erhöhung der Modellgüte
11.4.1 Logarithmieren
Erkennt man bleim Plotten der Daten, dass sich ein Großteil dieser in einem kleinen Bereich befindet, so kann es durchaus Sinn ergeben, den Bereich genauer zu betrachten. Wir “strecken” also den Bereich, indem wir die Daten logarithmieren.
Zum Überprüfen, ob sich ein logarithmieren lohnt, kann man geom_point() und geom_histogram() benutzen. Erkennt man z.B. in einem Histogramm, dass eine Verteilung schief ist, so lohnt sich das Logarithmieren.
iris_train %>%
select(where(is.numeric)) %>%
select(-id) %>%
pivot_longer(everything()) %>%
ggplot(., aes(x = value)) +
geom_histogram() +
facet_wrap(~ name, scales = "free_x")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.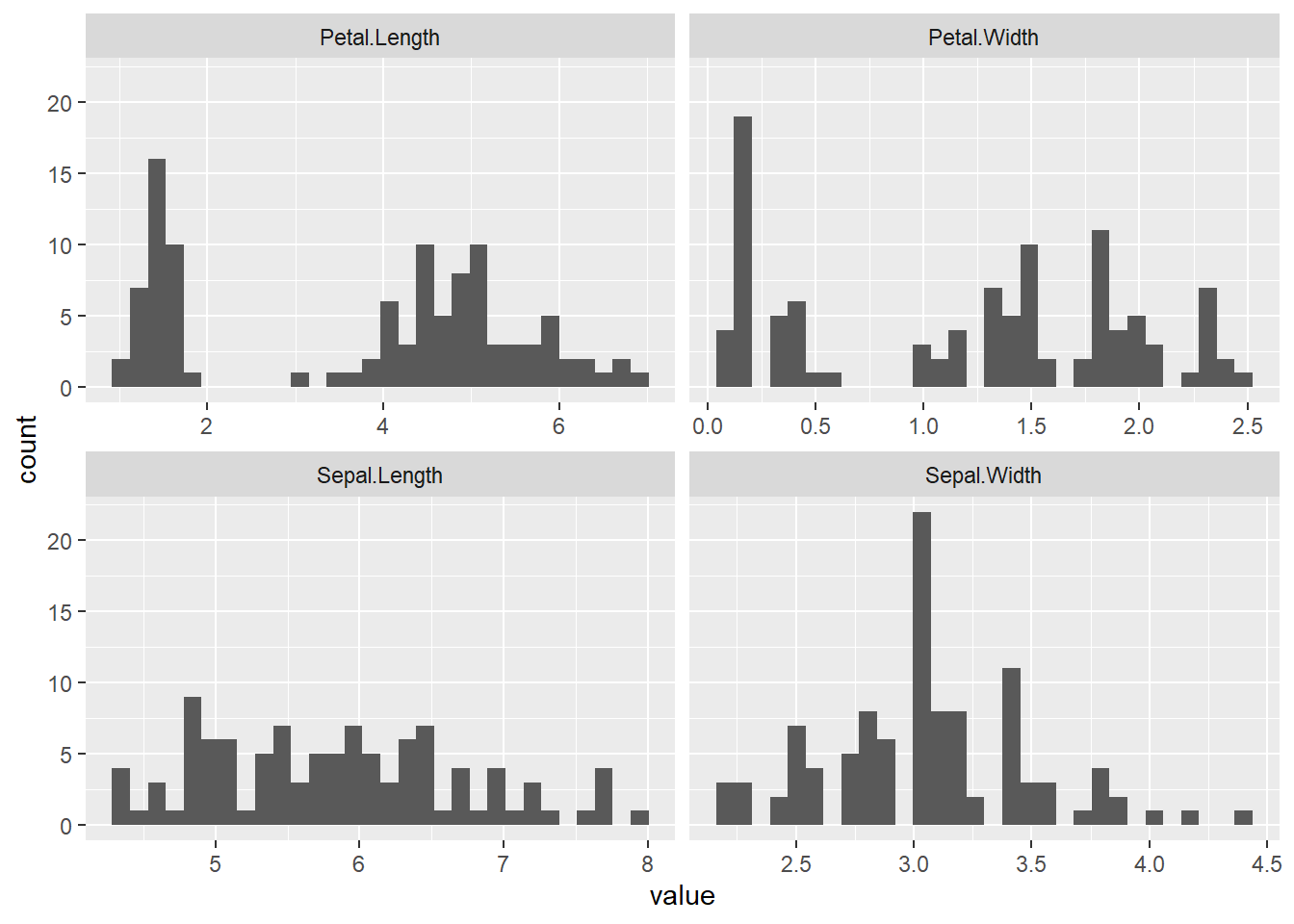
Hier bietet sich das Logarithmieren nicht unbedingt an. Man könnte höchstens Petal.Width logarithmieren, wenn man das möchte. Das Logarithmieren geht so:
iris_train <- iris_train %>%
mutate(Petal.Width_log = log(Petal.Width))Warnung: Logarithmiert man die Zahl 0, so kommt -Inf heraus. Das ist keine Zahl und macht daher Probleme.
11.4.2 Interaktionseffekt
Hängt die Steigung einer Regressionsgeraden ab von der Ausprägung eines anderen Prädiktors, so liegt ein Interaktionseffekt vor. Mit „abhängen” ist gemeint, dass die Veränderung in Y nicht gleich ist für alle Werte des Prädiktors X1, sondern sich je nach Wert eines anderen Prädiktors X2 unterscheidet. Um herauszufinden, ob zwischen Variablen ein Interaktionseffekt vorliegt, können wir folgenden Plot erstellen:
ggplot(iris_train, aes(x = Sepal.Length, y = Petal.Length, color = Species)) +
geom_point() +
geom_smooth(method = lm)`geom_smooth()` using formula = 'y ~ x'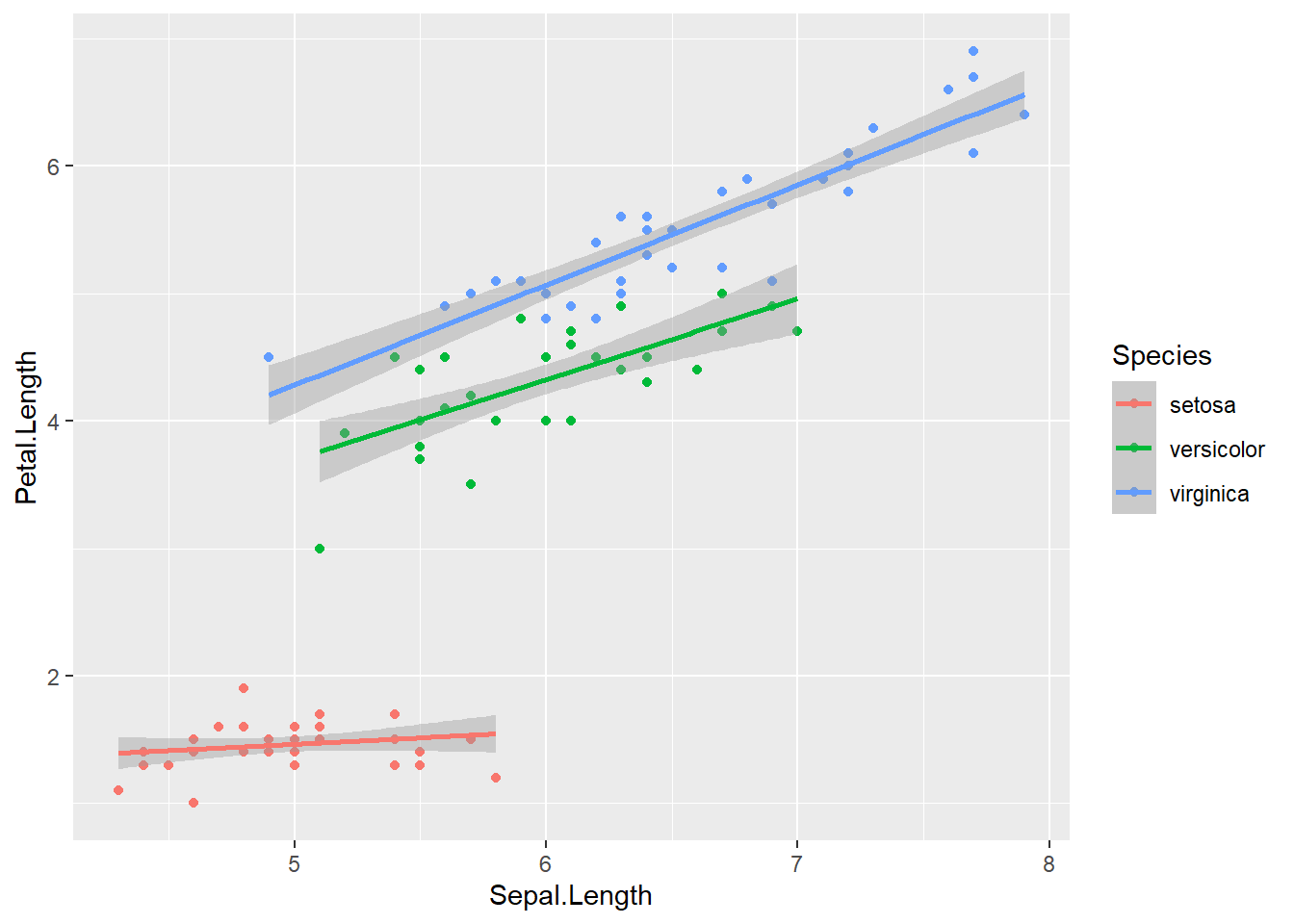
Wenn wir uns diesen Plot ansehen, erkennen wir, dass der Effekt von Petal.Length (X1) auf Sepal.Length (Y) abhängig ist von der Blütenart (X2), also von Species. Eine Steigerung von Petal.Length der Spezies Setosa führt zu einer geringeren Steigerung von Sepal.Length als bei den anderen Spezies. Es liegt hier also ein Interaktionseffekt zwischen den Prädiktoren Sepal.Length und Species vor, da die Geraden je nach Ausprägung von Specieseine unterschiedliche Steigung haben.
Im Modell bezieht man den Interaktionsefekt folgendermaßen mit ein:
lm3 <- lm(Sepal.Length ~ Petal.Length + Petal.Width + Petal.Length:Species,
data = iris_train)
summary(lm3)
Call:
lm(formula = Sepal.Length ~ Petal.Length + Petal.Width + Petal.Length:Species,
data = iris_train)
Residuals:
Min 1Q Median 3Q Max
-0.97281 -0.23124 -0.06142 0.22754 1.24191
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.7675 0.3449 8.025 2.01e-12 ***
Petal.Length 1.5332 0.2315 6.622 1.79e-09 ***
Petal.Width -0.2461 0.2053 -1.199 0.233416
Petal.Length:Speciesversicolor -0.7122 0.1685 -4.226 5.25e-05 ***
Petal.Length:Speciesvirginica -0.7501 0.1885 -3.980 0.000131 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3814 on 100 degrees of freedom
Multiple R-squared: 0.8168, Adjusted R-squared: 0.8095
F-statistic: 111.5 on 4 and 100 DF, p-value: < 2.2e-16Wir sehen: Das Modell ist gleich deutlich besser als davor.
11.5 Vorhersage
Nun erstellen wir mit dem Befehl predict() unsere Vorhersagen, also die Werte für Sepal.Length im Test-Datensatz und fügen sie als neue Spalte mit dem Namen preds hinzu. Wir predicten natürlich mit unserem besten Modell.
iris_test <- iris_test %>%
mutate(preds = predict(lm3, newdata = iris_test))Schließlich erstellen wir die wichtigste Datei für die Abgabe: Die csv-Datei, die neben den Vorhersagen auch die id-Spalte enthält, um die Vorhersagen den echten Werten zuordnen zu können.
abgabe <- iris_test %>%
select(id, preds)
write.csv(abgabe, file = "abgabe.csv", row.names = FALSE)