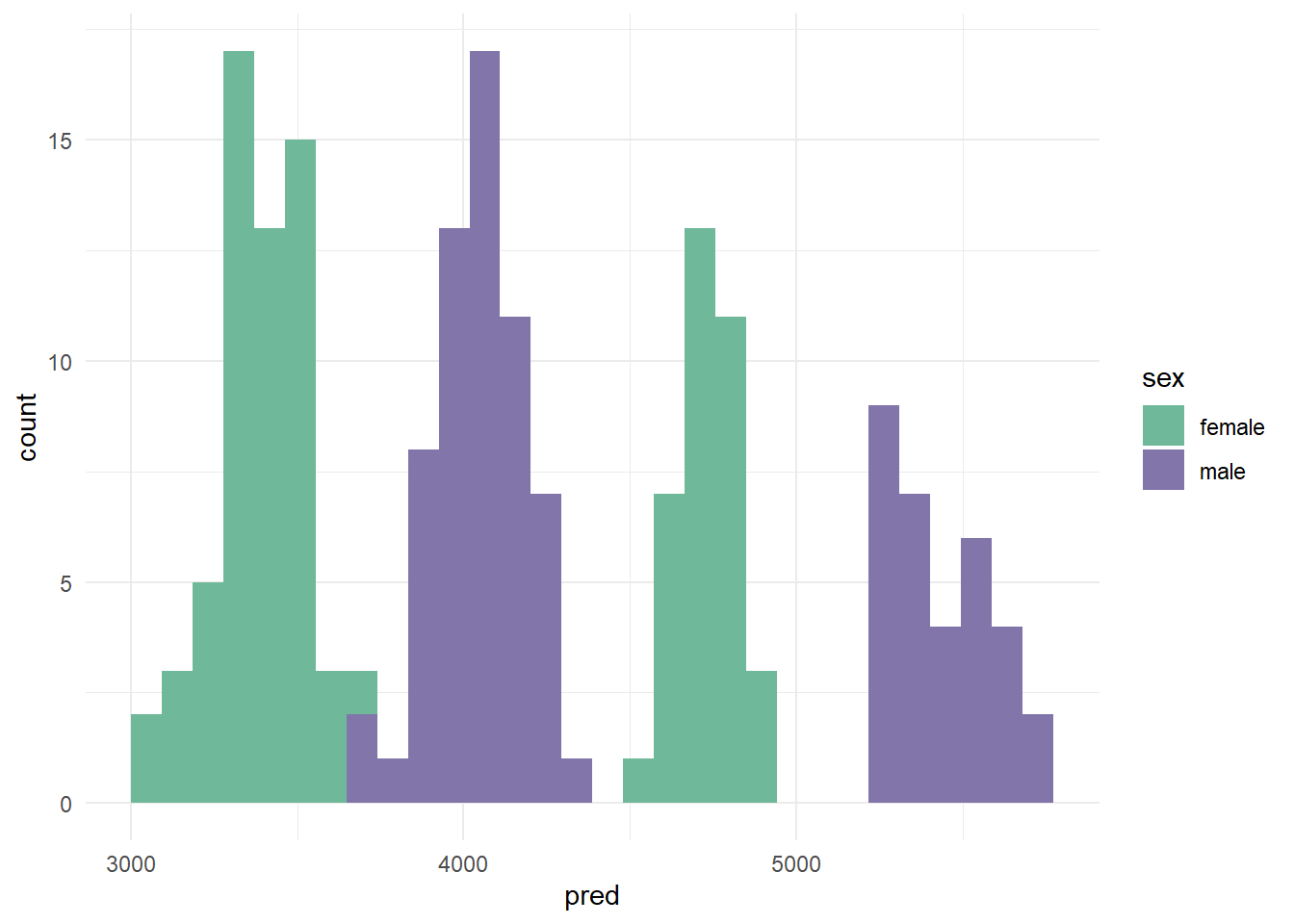12 Modellierung mit Aufteilung der Train-Daten

Author

Raphael Balzer

12.1 Einleitung

Im Folgenden wird die Vorhersagemodellierung noch einmal genauer behandelt. Um Overfitting zu vermeiden wird der Train-Datensatz aufgeteilt.

12.2 Pakte laden

library(rbthemes)
library(tidymodels) #für Auteilung der Daten reicht es, das Paket rsample zu laden

── Attaching packages ────────────────────────────────────── tidymodels 1.2.0 ──

✔ broom        1.0.5      ✔ recipes      1.0.10
✔ dials        1.2.1      ✔ rsample      1.2.1 
✔ dplyr        1.1.4      ✔ tibble       3.2.1 
✔ ggplot2      3.5.1      ✔ tidyr        1.3.1 
✔ infer        1.0.7      ✔ tune         1.2.1 
✔ modeldata    1.3.0      ✔ workflows    1.1.4 
✔ parsnip      1.2.1      ✔ workflowsets 1.1.0 
✔ purrr        1.0.2      ✔ yardstick    1.3.1

── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
✖ purrr::discard() masks scales::discard()
✖ dplyr::filter()  masks stats::filter()
✖ dplyr::lag()     masks stats::lag()
✖ recipes::step()  masks stats::step()
• Learn how to get started at https://www.tidymodels.org/start/

library(tidyverse)

── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ forcats   1.0.0     ✔ readr     2.1.5
✔ lubridate 1.9.3     ✔ stringr   1.5.1

── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ readr::col_factor() masks scales::col_factor()
✖ purrr::discard()    masks scales::discard()
✖ dplyr::filter()     masks stats::filter()
✖ stringr::fixed()    masks recipes::fixed()
✖ dplyr::lag()        masks stats::lag()
✖ readr::spec()       masks yardstick::spec()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

library(palmerpenguins)


Attache Paket: 'palmerpenguins'

Das folgende Objekt ist maskiert 'package:modeldata':

    penguins

penguins_data <- penguins

12.3 Daten importieren und aufteilen

Die folgende Aufteilung wird im Vorhinein vom Dozenten vorgenommen. In der Prüfung bekommt ihr d_train und d_test als Resultat des folgenden Codes:

penguins_data <- penguins_data %>% 
  drop_na() %>% 
  mutate(id = row_number()) %>% 
  select(id, everything())

set.seed(123)
train_test_split <- initial_split(penguins_data, prop = 0.7)
d_train <- training(train_test_split)
d_test <- testing(train_test_split)

Hier wird die Aufteilung des Train-Samples vorgenommen. Auf d_train1 werden Modelle trainiert, um dann auf d_train_test angewandt zu werden. So kann man sicherstellen, dass das Modell nicht nur die Daten, die es kennt, gut vorhersagt, sondern auch unbekannte Daten. Es gilt zu beachten, dass am Ende ein Modell abgegeben werden sollte, das auf dem kompletten ursprünglichen Train-Sample trainiert wurde.

dtrain_split <- initial_split(d_train, prop = 0.8)
d_train1 <- training(dtrain_split)
d_train_test <- testing(dtrain_split)

12.4 EDA

d_train %>% 
  group_by(sex) %>%
  summarise(mean(body_mass_g))

12.5 Vorhersagemodellierung

lm1 <- lm(body_mass_g ~ I(bill_depth_mm^2) + species + flipper_length_mm
         + bill_length_mm + sex, data = d_train1)
summary(lm1)


Call:
lm(formula = body_mass_g ~ I(bill_depth_mm^2) + species + flipper_length_mm + 
    bill_length_mm + sex, data = d_train1)

Residuals:
    Min      1Q  Median      3Q     Max 
-783.22 -171.88  -31.76  180.76  726.45 

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)        -617.0111   710.7614  -0.868 0.386503    
I(bill_depth_mm^2)    1.8207     0.7431   2.450 0.015245 *  
speciesChinstrap   -351.9506   114.5383  -3.073 0.002452 ** 
speciesGentoo       968.2548   167.9924   5.764 3.54e-08 ***
flipper_length_mm    13.2436     3.8255   3.462 0.000671 ***
bill_length_mm       26.2270    10.4342   2.514 0.012834 *  
sexmale             395.7132    66.2268   5.975 1.21e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 292.3 on 179 degrees of freedom
Multiple R-squared:  0.8696,    Adjusted R-squared:  0.8652 
F-statistic: 198.9 on 6 and 179 DF,  p-value: < 2.2e-16

lm2 <- lm(body_mass_g ~ flipper_length_mm + bill_depth_mm + bill_length_mm + sex, data = d_train1)
summary(lm2)


Call:
lm(formula = body_mass_g ~ flipper_length_mm + bill_depth_mm + 
    bill_length_mm + sex, data = d_train1)

Residuals:
    Min      1Q  Median      3Q     Max 
-921.34 -262.15    0.28  253.06  926.54 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -1543.865    883.423  -1.748   0.0822 .  
flipper_length_mm    36.896      3.440  10.726  < 2e-16 ***
bill_depth_mm       -95.565     22.281  -4.289 2.91e-05 ***
bill_length_mm       -7.090      7.042  -1.007   0.3154    
sexmale             585.857     74.296   7.885 2.85e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 358.6 on 181 degrees of freedom
Multiple R-squared:  0.8015,    Adjusted R-squared:  0.7972 
F-statistic: 182.8 on 4 and 181 DF,  p-value: < 2.2e-16

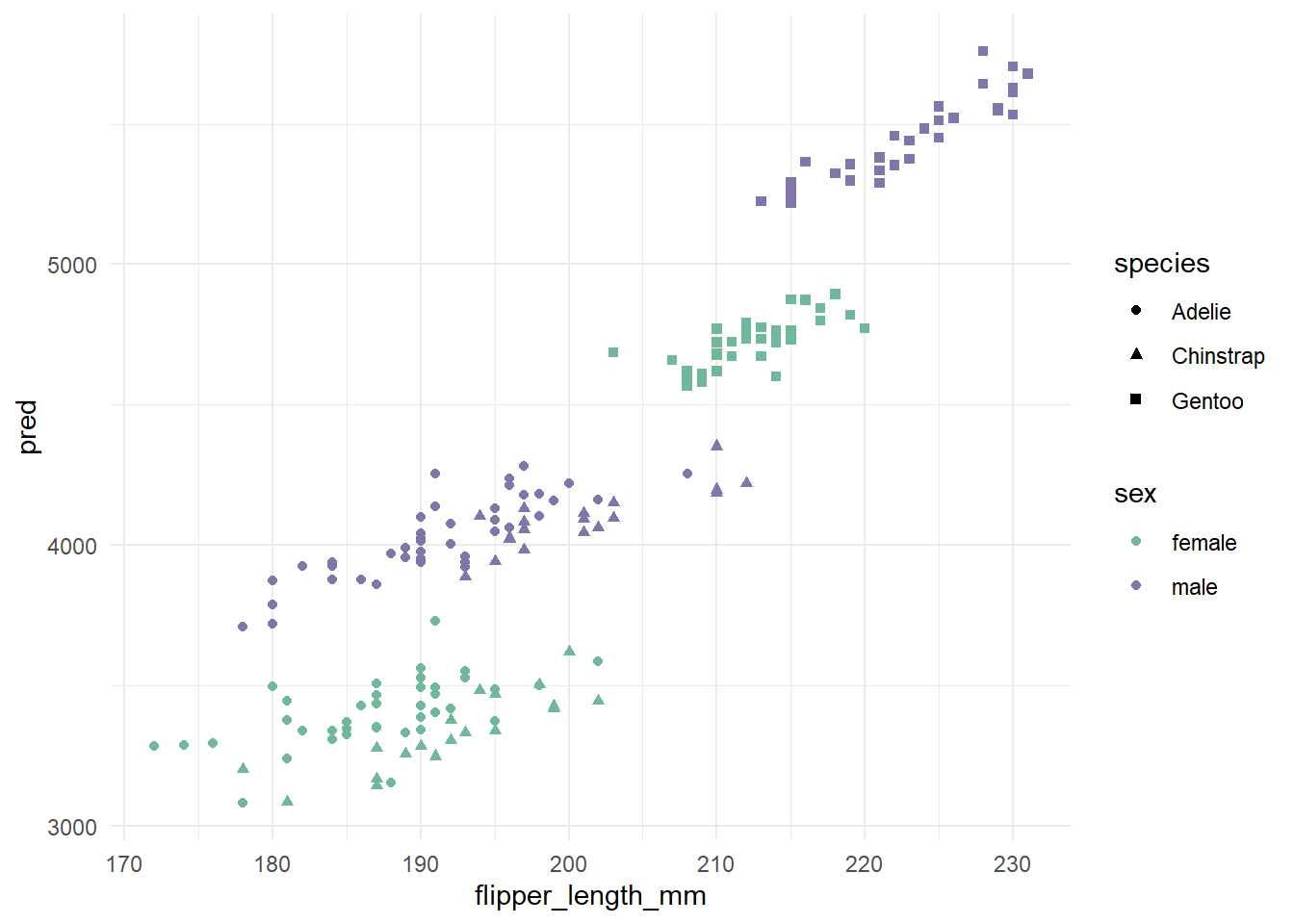
d_train1 <- d_train1 %>%
  mutate(pred = predict(lm1, newdata = d_train1))

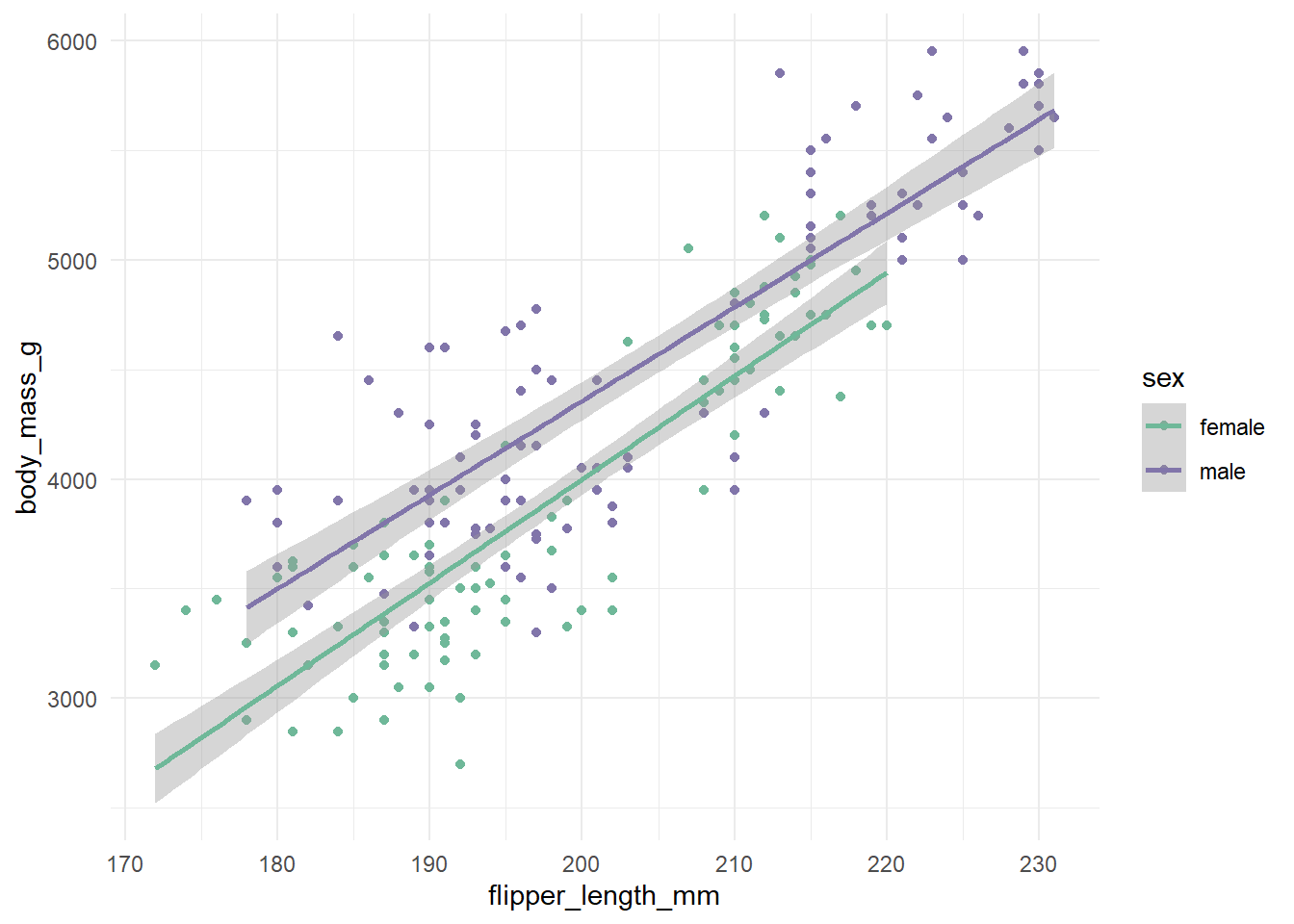
ggplot(data = d_train1, aes(x = flipper_length_mm, y = body_mass_g, color = sex)) +
  geom_point() +
  geom_smooth(method = "lm") +
  theme_pastel

`geom_smooth()` using formula = 'y ~ x'

ggplot(data = d_train1, aes(x = flipper_length_mm, y = pred)) +
  geom_point(aes(color = sex, shape = species)) +
  theme_pastel

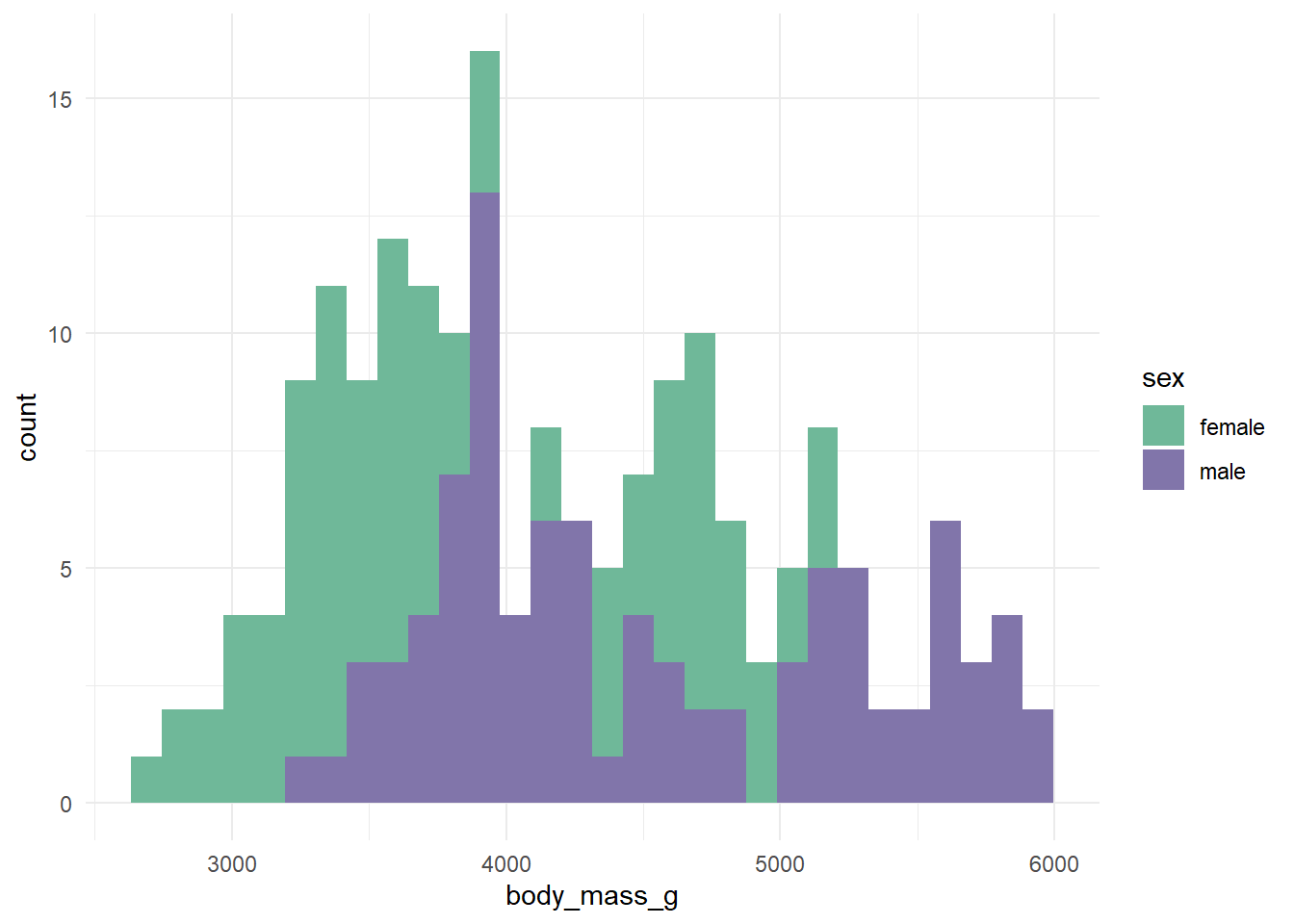
ggplot(data = d_train1, aes(x = body_mass_g, fill = sex)) +
  geom_histogram() +
  theme_pastel

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

ggplot(data = d_train1, aes(x = pred, fill=sex)) +
  geom_histogram() +
  theme_pastel

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

Zur Berechnung des RMSE kann auch die Funktion rmse() aus dem Paket performance verwendet werden. Hier wird manuell die Formel angewandt.

sqrt(mean((d_train1$pred - d_train1$body_mass_g)^2))

[1] 286.7817

Testen der Vorhersagegüte im eigenen Test-Sample:

d_train_test <- d_train_test %>%
  mutate(pred = predict(lm1, newdata = d_train_test))

sqrt(mean((d_train_test$pred - d_train_test$body_mass_g)^2))

[1] 232.8436

Für die eigene Abgabe trainieren wir unser bestes Modell noch einmal auf dem ganzen Train-Datensatz:

lm1 <- lm(body_mass_g ~ I(bill_depth_mm^2) + species 
         + flipper_length_mm
         + bill_length_mm + sex, data = d_train)
summary(lm1)


Call:
lm(formula = body_mass_g ~ I(bill_depth_mm^2) + species + flipper_length_mm + 
    bill_length_mm + sex, data = d_train)

Residuals:
    Min      1Q  Median      3Q     Max 
-811.87 -155.90  -24.31  162.38  912.30 

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)        -938.6799   604.1940  -1.554 0.121677    
I(bill_depth_mm^2)    2.0075     0.6394   3.140 0.001917 ** 
speciesChinstrap   -322.7564    92.4227  -3.492 0.000576 ***
speciesGentoo       968.6972   141.3086   6.855 6.71e-11 ***
flipper_length_mm    14.6584     3.3034   4.437 1.42e-05 ***
bill_length_mm       25.6652     8.4080   3.052 0.002541 ** 
sexmale             391.6317    56.1159   6.979 3.26e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 280.4 on 226 degrees of freedom
Multiple R-squared:  0.883, Adjusted R-squared:  0.8799 
F-statistic: 284.2 on 6 and 226 DF,  p-value: < 2.2e-16

Berechnung der Note (für euch in der Klausur nicht möglich):

d_test <- d_test %>%
  mutate(preds = predict(lm1, newdata = d_test))

sqrt(mean((d_test$preds - d_test$body_mass_g)^2))

[1] 308.0294

Erstellung der Abgabe-Csv:

abgabe <- d_test %>% 
  select(id, preds)
write_csv(abgabe, "abgabe_notebook.csv")